funciones computables reducibilidad de turing

funciones computables

las funciones computables   son una formulacion de la intuitiva de algoritmo segun Church -Turing son exatamente las funciones que puede ser calculadas con una maquina de calculo.

las funciones computables son usadas para discutir computabilidad sin referise a ningun modelo de computacion concreto, como maquina de Turing o maquina de registro. los axiomas de Blum puede ser usados para definir una teoria de complejidad computacional abstracta sobre sobre el congunto de funciones computables.

en la teoria complejidad computacional, el problema de determinar la complegidad de uana funcion computable esta conocido como un problema de funciones.

Una funcion parcial se llama computable si el grafico de f es un conjunto recursivamente enumerable. el comjunto de funciones parciales computables con un parametro es normalmente escrito

Definición

Una función parcial

se llama parcialmente computable si el gráfico de f es un conjunto recursivamente enumerable. El conjunto de funciones parcialmente computables con un parámetro es normalmente escrito o si el número de parámetros puede deducirse del contexto.
Una función total

se llama computable si el gráfico de f es un conjunto recursivo. El conjunto de funciones totalmente computables con un parámetro normalmente se escribe o .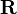
Una función computable f se llama predicado computable si es una función con valor booleano, es decir

A veces, por razones de claridad, se escribe una función computable como

Podemos fácilmente codificar g en una nueva función

usando una función de parciales.

Reducibilidad de Turing

la  nicion mas fundamental de la reducibilidad es un sistema A de número naturales está Turing reducible a un sistema B si y solamente si hay máquina de Turing del oráculo eso, cuando está funcionado con B pues su sistema del oráculo, computará función del indicador (función característica) de A. Equivalente, A es Turing reducible a B si y solamente si hay un algoritmo para computar la función del indicador para A a condición de que es el algoritmo se proporciona los medios de contestar correctamente a las cuestiones de la forma “ n en B?".

La reducibilidad de Turing sirve como línea que se divide para otras nociones de la reducibilidad porque, según Tesis de la Iglesia-Turing, es la relación más general de la reducibilidad que es eficaz. Las relaciones de la reducibilidad que implican la reducibilidad de Turing han venido ser conocidas como reducibilities fuertes, mientras que son los que son implicadas por la reducibilidad de Turing reducibilities débiles. Equivalente, una relación fuerte de la reducibilidad es una que grados forman una relación de equivalencia más fina que los grados de Turing, mientras que una relación débil de la reducibilidad es una que grados forman una relación de equivalencia más gruesa que la equivalencia de Turing.

Reducciones más fuertes que la reducibilidad de Turing

Los reducibilities fuertes incluyen

• Reducibilidad de One-one: A es el one-one reducible a B si hay una función computable del one-one f con A(x) = B(f(x)) para todos x.
• Mucho-uno reducibilidad: A está mucho-uno reducible a B si hay una función computable f con A(x) = B(f(x)) para todos x.
• Verdad-tabla reducible: A es la verdad-tabla reducible a B si A es Turing reducible a B vía una sola (oráculo) máquina de Turing que produce una función total concerniente a cada oráculo.
• Verdad-tabla débil reducible: A es la verdad-tabla débil reducible a B si hay una reducción de Turing de B a A y una función recurrente f cuál limita uso. Siempre que A es la verdad-tabla reducible a B, A está también la verdad-tabla débil reducible a B, puesto que uno puede construir un límite recurrente en el uso considerando el uso máximo en cualquier oráculo, que sea computable si la reducción es total en todos los oráculos.
• Reducible positivo: A está reducible positivo a B si y solamente si A es la verdad-tabla reducible a B de una manera que una puede computar para cada x átomos que consisten en de un fórmula de la forma B(0), B(1), ... tales que estos átomos están combinados cerca y y o, donde y de a y b es 1 si a = 1 y b = 1 y así sucesivamente.
• Reducible disyuntivo: Similar a reducible positivo con el constreñimiento adicional que solamente o se permiten.
• Reducibilidad conjuntiva: Similar a la reducibilidad positiva con el constreñimiento adicional que solamente y se permiten.
• Reducibilidad linear: Similar a la reducibilidad positiva pero con el constreñimiento ese todos los átomos de la forma B(n) son combinados por exclusiva o. Es decir A está reducible linear a B si y solamente si cálculos de una función computable para cada uno x un sistema finito F(x) dado como lista explícita de números tales que x ∈ A si y solamente si F(x) contiene un número impar de elementos de B.